
典型例題
【例1】如圖���,在平面直角坐標(biāo)系中,⊙P的圓心坐標(biāo)是(3��,a)(a>3)�,半徑為3��,函數(shù)y=x的圖象被⊙P截得的弦AB的長為��,則a的值是( )
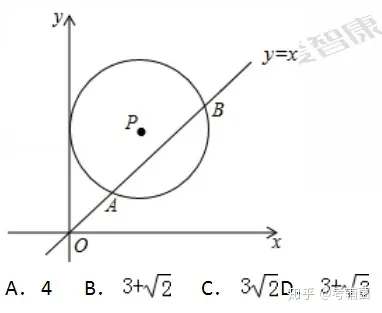
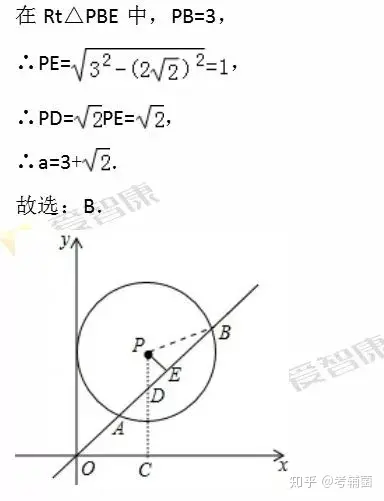
【分析】本題考查的是圓的垂徑定理��,同時(shí)也考查了勾股定理和等腰直角三角形的性質(zhì).我們可以做PC⊥x軸于C,交AB于D����,作PE⊥AB于E�,連結(jié)PB,由于OC=3���,PC=a���,求得D點(diǎn)坐標(biāo),判斷△OCD��,△PED的形狀.由PE⊥AB�,根據(jù)垂徑定理得AE=BE=AB=2�����,在Rt△PBE中����,利用勾股定理可計(jì)算出結(jié)果���。
答案

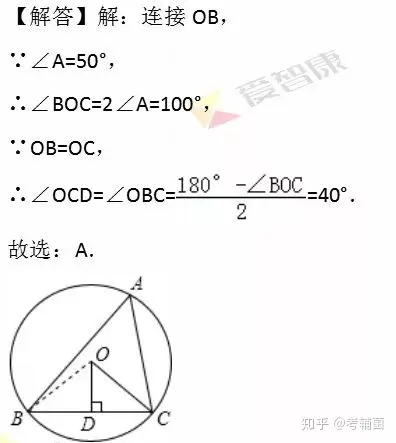
【例2】如圖�,△ABC內(nèi)接于⊙O���,OD⊥BC于D,∠A=50°��,則∠OCD的度數(shù)是( )
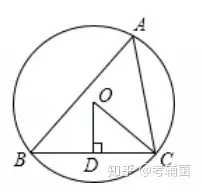
A.40° B.45° C.50° D.60°
【分析】此題考查了圓周角定理與等腰三角形的性質(zhì).難度不大���,需要注意掌握在同圓或等圓中,同弧或等弧所對的圓周角等于這條弧所對的圓心角的一半定理的應(yīng)用����。首先連接OB��,由在同圓或等圓中����,同弧或等弧所對的圓周角等于這條弧所對的圓心角的一半�����,即可求得∠BOC的度數(shù)���,又由OB=OC,根據(jù)等邊對等角的性質(zhì)��,即可求得∠OCD的度數(shù).
答案
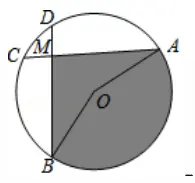
【例3】(2016秋•杭州期末)如圖�,在⊙O中�,弦AC,BD相交于點(diǎn)M�,且∠A=∠B
(1)求證:AC=BD;
(2)若OA=4�����,∠A=30°�����,當(dāng)AC⊥BD時(shí)��,求:
①弧CD的長;
②圖中陰影部分面積.
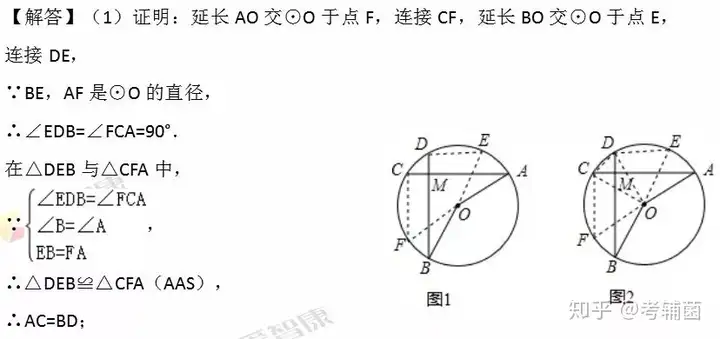
【分析】這道題目考查的是垂徑定理,扇形面積的計(jì)算����,以及全等三角形的判斷和性質(zhì),我們需要根據(jù)題意作出輔助線��,構(gòu)造出直角三角形是解答此題的關(guān)鍵.第一問可以延長AO交⊙O于點(diǎn)F,連接CF��,延長BO交⊙O于點(diǎn)E���,連接DE��,根據(jù)圓周角定理得出∠EDB=∠FCA=90°,故可得出△DEB≌△CFA����,由此得出結(jié)論;
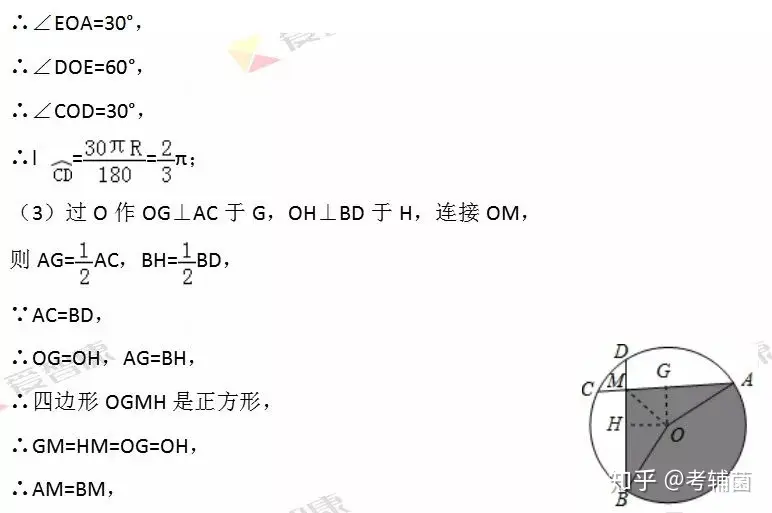
第二問第一小問延長AO交⊙O于點(diǎn)F���,連接CF����,延長BO交⊙O于點(diǎn)E�����,連接DE,CD����,OD�,OC����,求出∠COA的度數(shù)���,再由三角形外角的性質(zhì)得出∠EOA的度數(shù),由弧長公式即可得出結(jié)論;第二小問過O作OG⊥AC于G���,OH⊥BD于H,連接OM����,根據(jù)垂徑定理得到AG=AC����,BH=BD,推出四邊形OGMH是正方形����,根據(jù)正方形的性質(zhì)得到GM=HM=OG=OH,得到AM=BM��,解直角三角形得到相關(guān)長度,根據(jù)全等三角形的性質(zhì)得到∠B�����,求得∠AOB度數(shù)�,得到結(jié)果.
答案


變式練習(xí)
【練習(xí)1】如圖��,矩形ABCD與圓心在AB上的⊙O交于點(diǎn)G��、B���、F���、E�,GB=8cm�����,AG=1cm����,DE=2cm�����,則EF= cm.
【練習(xí)2】如圖����,四邊形ABCD中��,AB=AC=AD�,若∠CAD=76°���,則∠CBD= 度.
【練習(xí)3】如圖,CD是⊙O的直徑����,弦AB⊥CD,垂足為點(diǎn)M���,AB=20�����,分別以CM、DM為直徑作兩個大小不同的⊙O1和⊙O2��,則圖中陰影部分的面積為 (結(jié)果保留π).
【練習(xí)4】如圖,等腰Rt△ABC的直角邊長為4��,以A為圓心�����,直角邊AB為半徑作弧BC1,交斜邊AC于點(diǎn)C1��,C1B1⊥AB于點(diǎn)B1��,設(shè)弧BC1�����,C1B1���,B1B圍成的陰影部分的面積為S1,然后以A為圓心���,AB1為半徑作弧B1C2�,交斜邊AC于點(diǎn)C2�����,C2B2⊥AB于點(diǎn)B2,設(shè)弧B1C2�����,C2B2���,B2B1圍成的陰影部分的面積為S2,按此規(guī)律繼續(xù)作下去���,得到的陰影部分的面積S3=.
答案
【練習(xí)1】6
【練習(xí)2】38
【練習(xí)3】50π
【練習(xí)4】
歡迎使用手機(jī)、平板等移動設(shè)備訪問中考網(wǎng)�,2023中考一路陪伴同行���!>>點(diǎn)擊查看


















