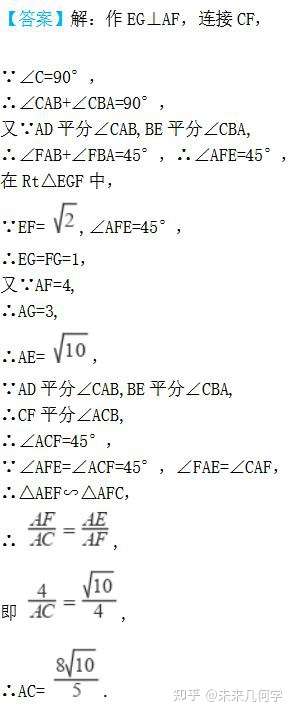│§ųąÄū║╬ę╗ų▒╩Ū▓╗╔┘═¼īW▒╚▌^Ņ^╠█Ą─å¢Ņ}ĪŻį┌ūC├„Äū║╬Ņ}ĢrŻ¼šę▓╗£╩ĘĮŽ“���Ż¼ęįų┴ė┌Ū¦Ņ^╚fŠwŻ¼▓╗ų¬Å─║╬╚ļ╩ų;╔§ų┴ęįŪ░ū÷▀^Ą─Ņ}Ż¼ę▓╚ń▀^č█įŲ¤¤�ĪŻ
▀@╩Ū╩▓├┤įŁę“?
╬ęšJ×ķ╩Ūø]ėąšŲ╬šöĄ(sh©┤)īWīW┴ĢĄ─ĘĮĘ©�����ĪŻį┌▀@└’╬ęŽ╚║åå╬Ą─ĮķĮBŽ┬╬ęūį╝║Ą─öĄ(sh©┤)īWīW┴ĢŪķør(─Ńéāę▓┐╔ęį└ĒĮŌ×ķ╬ę▀m«ö?sh©┤)─┤ĄćuŽ┬ūį╝║)Ż║ąĪīW║═│§ųąöĄ(sh©┤)īW├┐┤╬┐╝įćę¬├┤╩ŪØMĘųę¬├┤╩ŪĮėĮ³ØMĘų;Ė▀ųąš²║├ė÷ĄĮ╬ęĄ─ŪÓ┤║┼č─µŲ┌�Ż¼öĄ(sh©┤)īW│╔┐āėą╦∙Ž┬╗¼;Ą½ĄĮ┴╦┤¾īWęį║¾����Ż¼öĄ(sh©┤)īW│╔┐āėų═╗’w├═▀M;蹊┐╔·šą╔·┐╝įćŻ¼öĄ(sh©┤)īW┐╝┴╦139Ęų(ØMĘų150�����Ż¼139į┌«ö─Ļšµ╦ŃĄ─╔Ž╩Ū║▄Ė▀Ą─ĘųöĄ(sh©┤)�����Ż¼ų▄ć·║▄ČÓŲĮĢr│╔┐ā║▄║├Ą─═¼īW▀B90ĘųČ╝ø]ėą)Ą─║├│╔┐ā;2019─Ļģó╝ėĖ▀ųąĮ╠Ĥ┘YĖ±ūC┐╝įć���Ż¼ę╗┤╬ąį═©▀^(«öĢrėąę╗éĆ87╚╦┐╝│§Ė▀ųąöĄ(sh©┤)īWĮ╠Ĥ┘YĖ±ūCĄ─╬óą┼╚║����Ż¼āH╚²╚╦═©▀^Ż¼┴Ē═Ōā╔éĆ═©▀^Ą─╩Ū│§ųąĮ╠Ĥ┘YĖ±ūC)�Ż¼ę¬ų¬Ą└▀@ļx╬ę2008─Ļ┤T╩┐«ģśI(y©©)Ż¼ęčĮø(j©®ng)11─Ļ▀^╚ź┴╦�ĪŻ11─Ļø]┐┤▀^öĄ(sh©┤)īWŻ¼ę╗┤╬ąį═©▀^Ė▀ųąöĄ(sh©┤)īWĮ╠Ĥ┘YĖ±ūC┐╝įć(║¼│§ųą����ĪóĖ▀ųąĪó┤¾īWā╚(n©©i)╚▌)�Ż¼╩Ū╩▓├┤Ė┼─Ņ?╩Ūę“×ķ╬ęöĄ(sh©┤)īW╗∙ĄA(ch©│)į·īŹĘĆ(w©¦n)╣╠Ż¼11─ĻČ╝ø]į§├┤═³ėø�ĪŻę▓Š═╩Ūšfų╗ę¬─·īW┴ĢĘĮĘ©Ą├«öŻ¼šµš²└ĒĮŌ┴╦öĄ(sh©┤)īWĖ┼─Ņ���Ż¼╝┤╩╣▀^į┘Š├ōņŲüĒę▓ĘŪ│Ż╚▌ęū����ĪŻ
║├�Ż¼▐D(zhu©Żn)╗žš²Ņ}ĪŻ
Äū║╬▓╗āHāH╩Ū│§ųąöĄ(sh©┤)īWĄ─ųž³c�����Ż¼į┌Ė▀ųąöĄ(sh©┤)īWųąę▓š╝ėąŽÓ«ö┤¾Ą─▒╚ųžŻ¼ŲõļyČ╚│╩┬▌ą²╩Į╔Ž╔²����Ż¼╦∙ęį│§ųąÄū║╬╗∙ĄA(ch©│)ę╗Č©ę¬┤“║├ĪŻ║├į┌│§ųąÄū║╬ūā╗»▓ó▓╗ČÓ�����Ż¼┤¾═¼ąĪ«É�����Ż¼ų╗꬚Ų╬š┴╦īW┴Ģ╗“╦╝┐╝Ą─ĘĮĘ©���Ż¼ąĪĄ─▓Ņ«É┼eę╗Ę┤╚²Ż¼┤¾ČÓöĄ(sh©┤)Äū║╬Ņ}▒ŃėŁ╚ąČ°ĮŌ�����ĪŻ
īW║├öĄ(sh©┤)īW▓╗Ę┴Ęų×ķęįŽ┬Äū▓Į�����Ż¼╚ń╣¹─Ń─▄ūxČ«▓ół╠(zh©¬)ąąŻ¼90%Ą─Ņ}─┐─▄ę╗ĘųńŖų«ā╚(n©©i)╔§ų┴Äū├ļńŖų«ā╚(n©©i)│÷ĮŌŅ}╦╝┬Ę���Ż¼ŽÓą┼─ŃĄ─öĄ(sh©┤)īW│╔┐āĢ■ėą┘|(zh©¼)Ą─’w▄S!
Ą┌ę╗▓ĮŻ║└╬ėøĖ┼─Ņ��ĪóČ©└Ē�����Īóąį┘|(zh©¼)
║▄ČÓ╝ęķL�����Īó└ŽÄ¤ų╗ų¬Ą└ūīūį╝║║óūė╗“?q©▒)W╔·ČÓ╦óŅ}��Ż¼īŹąąŅ}║Żæ(zh©żn)ąg(sh©┤)�����Ż¼Ą½╩Ū╦¹éā▓╗ŪÕ│■ūį╝║Ą─║óūė╔§ų┴▀Bšn▒Š╔ŽĄ─╗∙▒ŠĖ┼─ŅČ╝ŽĪ└’║²═┐����ĪŻę╗╬ČĄ─ū÷Ņ}�����Ż¼░č║óūė┼¬Ą├╔Ēą─ŠŃŲŻ▓╗šfŻ¼╔§ų┴Ģ■«a(ch©Żn)╔·Ąųė|ŪķŠw��ĪŻĄĮūŅ║¾ę└╚╗ų╗Ģ■ū÷ą®║åå╬Ą─Ņ}─┐���Ż¼ī”ė┌▌^ļyĄ─Ņ}─┐�����Ż¼ų╗ę¬╔į╬óėąą®ūā╗»����Ż¼ę└╚╗▓╗Ģ■���Ż¼▀@śėĢ■╩╣║óūėųØu╩¦╚źī”öĄ(sh©┤)īWīW┴ĢĄ─┼d╚ż�����ĪŻšfīŹįÆ����Ż¼▀@śėĄ─╝ęķL║═└ŽÄ¤▓╗į┌╔┘öĄ(sh©┤)ĪŻ
ŲõīŹ┤¾▓┐Ęų┐┤╦Ų▌^ļyĄ─Ņ}─┐Č╝╩ŪÅ─╗∙▒ŠĄ─Č©┴x����ĪóČ©└Ē║═ąį┘|(zh©¼)╚ļ╩ų�Ż¼▓╗ą┼?ę╗Ģ■┼eÄūéĆ└²ūė─Ń┐┤┐┤Š═ų¬Ą└┴╦�ĪŻ
─Ū├┤╚ń║╬▓┼─▄╩ņŠÜĄ─šŲ╬š▀@ą®ūŅ╗∙▒ŠĄ─ų¬ūR─ž?╬ęšJ×ķąĶę¬ū÷║├ęįŽ┬╚²³cŻ║1Īó╩ņūxĮ╠▓─����Ż¼└ĒĮŌ▀@ą®Ė┼─ŅĄ─┤·öĄ(sh©┤)║═Äū║╬ęŌ┴x;2Īó╩ņ▒│Č©┴xČ©└Ēąį┘|(zh©¼)(šlšföĄ(sh©┤)īW▓╗ė├▒│Ą─?ļmšf▓╗Ž±šZ╬─ėóšZ▒│Ą──Ū├┤ČÓ��Ż¼«ö╚╗▓╗╩Ū╦└ėøė▓▒│�����Ż¼Č°╩Ūį┌└ĒĮŌĄ─╗∙ĄA(ch©│)╔Ž╚ź▒│šb);3��Īóū÷Ņ}Ą─▀^│╠ųąę¬ŪÕ│■├┐ę╗Ņ}æ¬(y©®ng)ė├┴╦╩▓├┤Ė┼─ŅČ©└Ē║═ąį┘|(zh©¼)��ĪŻ
╚ń╣¹─▄└╬ėø▓óšŲ╬šĖ┼─Ņ�����ĪóČ©└Ē���Īóąį┘|(zh©¼)�����Ż¼ū÷ĄĮęį╔Ž╚²³c��Ż¼─Ū├┤╣¦Ž▓─Ń���Ż¼─Ń▀_ĄĮ┴╦╝░Ė±ŠĆ�����Ż¼ę▓Š═╩Ūšf┐╝įćØMĘų100Ęų�����Ż¼─Ń─▄Ą├éĆ60Ęų╩Ū▓╗│╔å¢Ņ}Ą─�ĪŻ

│§ųąÄū║╬
«ö╚╗╬ęéāĮ^┤¾▓┐Ęų═¼īW▓╗ØMūŃ60ĘųĄ─╝░Ė±│╔┐ā�Ż¼─Ūį§├┤▐k?▓╗╝▒Ż¼╬ęéā└^└m(x©┤)┐┤Ą┌Č■▓ĮŻ║
Ą┌Č■▓ĮŻ║╚ń║╬╚ź╦╝┐╝?
║▄ČÓīW╔·┼÷ĄĮ▌^×ķņ`╗Ņ╗“╔įėąļyČ╚Ą─Ņ}─┐�Ż¼Ū¦Ņ^╚fŠwŻ¼░┘╦╝─¬ĮŌ�ĪŻ▀@ŲõīŹ╩Ūę“×ķø]ėąūźūĪ│§ųąÄū║╬Ą─▒Š┘|(zh©¼)�Ż¼ęį╝░╦╝┐╝Ą─ĘĮĘ©ĪŻīŹļH╔Ž║▄ČÓŅ}ē║Ė∙Š═▓╗ė├─Ńį§├┤╚ź╦╝┐╝Ż¼ų╗ę¬─ŃšŲ╬š┴╦ę╗éĆ╣╠Č©Ą─ĮŌŅ}ĘĮĘ©�ĪŻ
╬ęéāŽ╚üĒ┴╦ĮŌ│§ųąÄū║╬Ą─▒Š┘|(zh©¼)——│§ųąļAČ╬Ą─┤¾ČÓöĄ(sh©┤)öĄ(sh©┤)īWÄū║╬Ņ}�����Ż¼▒Š┘|(zh©¼)╔ŽČ╝╩Ūī”ŠĆ╗“ĮŪų«ķgĻP(gu©Īn)ŽĄĄ─╠Ä└Ē��ĪŻėøūĪ�Ż¼į┘ÅŖš{(di©żo)ę╗▒ķŻ║ŠĆ╗“ĮŪ(ŠĆ┼cŠĆ�����ĪóŠĆ┼cĮŪ��ĪóĮŪ┼cĮŪ)ų«ķgĻP(gu©Īn)ŽĄĄ─╠Ä└Ē���ĪŻ
ę▓Š═╩Ūšf���Ż¼╚ń╣¹į┌ĮŌŅ}Ą─▀^│╠ųą���Ż¼ėąęŌūRĄž╚źšę┼cŚl╝■╗“ĮY(ji©”)šōŽÓĻP(gu©Īn)Ą─ĮŪ╗“ŠĆĄ─ĻP(gu©Īn)ŽĄŻ¼įĮČÓįĮ║├��Ż¼╦╝┬Ę═©│Ż║▄┐ņūį╚╗Č°╚╗Š═│÷üĒ┴╦ĪŻę╗░ŃŪķørŽ┬��Ż¼ĮŌŅ}ĢrąĶꬎ╚šę│÷═╗ŲŲ┐┌���Ż¼═╗ŲŲ┐┌į┌──?Š═╩ŪŅ}─┐ųąĄ─ĻP(gu©Īn)µIšZŠõĪŻ
║├�����Ż¼╬ęéāüĒ┐┤Ž┬├µ▀@Ą└└²Ņ}Ż║
└²1�����Īó╚ńłD�Ż¼į┌ŲĮąą╦─▀ģą╬ABCDųąŻ¼E╩ŪAB╔Žę╗³c����Ż¼DEĪóCEĘųäe╩Ū∠ADC�����Īó∠BCDĄ─ŲĮĘųŠĆ.╚¶AD=5�����Ż¼DE=6�Ż¼ätŲĮąą╦─▀ģą╬ABCDĄ─├µĘe╩Ū()
└²1 łD1-1
A.96 B.60 C.48 D.30
ĪŠ╦╝┐╝Ī┐▀@ę╗Ņ}╩Ūūī╬ęéāŪ¾ŲĮąą╦─▀ģą╬ABCDĄ─├µĘeĪŻ╬ęéāūŅ╚▌ęūŽļĄĮ╩Ū╣½╩ĮĘ©Ż║ Ąū×Ė▀;Ą┌Č■ĘNĘĮĘ©Ż║ę▓┐╔ęį▐D(zhu©Żn)╗»×ķÄūéĆ╚²ĮŪą╬Ą─├µĘe║═����Ż¼Č°Ū¾╚²ĮŪą╬Ą─├µĘe╣½╩Į╩ŪĄū×Ė▀÷2Ī��Ż┐┤┐┤▀@ā╔ĘNĘĮĘ©▒Š┘|(zh©¼)╔ŽČ╝╩ŪŠĆ┼cŠĆĄ─ĻP(gu©Īn)ŽĄ�ĪŻ
─Ū╬ęéāŠ═čžų°▀@Ślų„ŠĆ▐D(zhu©Żn)╗»Ņ}─┐ųąĄ─├┐éĆŚl╝■Ż║╬ęéā┐┤ĄĮŚl╝■ųąĻP(gu©Īn)µIšZŠõ╩ŪĮŪŲĮĘųŠĆŻ¼─Ū├┤╬ęéā▓╗ė├╚ź╦╝┐╝����Ż¼ų▒ĮėŠ═└¹ė├ĮŪŲĮĘųŠĆĄ─ąį┘|(zh©¼)Ż¼░č╦∙ėąŽÓĄ╚Ą─ĮŪś╦ėø│÷üĒ����ĪŻėą═¼īWę▓įSĢ■å¢����Ż¼╬ęéāŪ¾Ą─╩ŪŠĆ┼cŠĆĄ─ĻP(gu©Īn)ŽĄ����Ż¼ś╦│÷ŽÓĄ╚Ą─ĮŪėą╩▓├┤ė├?įŁę“į┌ė┌Ż║ę╗ĪóŅ}─┐ųąūŅĻP(gu©Īn)µIĄ─šZŠõų╗ėąĮŪŲĮĘųŠĆ�Ż¼╬ęéāų╗ėą└¹ė├ĮŪŲĮĘųŠĆĄ─ąį┘|(zh©¼)▓╗╩Ū?Č■ĪóĮŪĄ─ĻP(gu©Īn)ŽĄ║▄ČÓĢr║“Č╝┐╔ęį▐D(zhu©Żn)╗»│╔ŠĆ┼cŠĆĄ─ĻP(gu©Īn)ŽĄ░Ī����Ż¼ūŅ│Żė├Ą─Ą╚č³╚²ĮŪą╬ā╔č³ŽÓĄ╚▓╗╩Ūåß?
║├Ż¼└¹ė├ĮŪŲĮĘųŠĆĄ─ąį┘|(zh©¼)���Ż¼╬ęéāį┌łDųąś╦│÷EDīó∠ADCĘų×ķā╔éĆŽÓĄ╚Ą─∠1���Ż¼ECīó∠DCBĘų×ķā╔éĆŽÓĄ╚Ą─∠2ĪŻ─Ū├┤▀@śė╬ęéā╩Ūʱ░č╦∙ėąŽÓĄ╚Ą─∠1║═∠2Č╝ś╦│÷üĒ┴╦?’@╚╗▓╗╩Ū!ę“×ķ╬ęéā┐╔ęį┐┤ĄĮų╗ś╦│÷▀@ā╔ī”ŽÓĄ╚Ą─ĮŪø]ėąė├�Ż¼▀Ć╩ŪĮŌ▓╗│÷üĒĪŻ─Ū├┤╬ęéāšJšµūxę╗Ž┬Ņ}─┐Śl╝■��Ż¼░l(f©Ī)¼F(xi©żn)┐╔ęįį┘Ė∙ō■(j©┤)ŲĮąą╦─▀ģą╬ā╔ī”▀ģŲĮąąĄ─ąį┘|(zh©¼)����Ż¼ś╦│÷łDųą╦∙ėą┼c∠1║═∠2ŽÓĄ╚Ą─ĮŪ�����ĪŻ
─Ū▀@┼cŲĮąą╦─▀ģą╬├µĘeėą╩▓├┤ĻP(gu©Īn)ŽĄ─ž?╬ęéāį┘Ė∙ō■(j©┤)äé▓┼Ū¾Ą├ŽÓĄ╚Ą─ĮŪ▐D(zhu©Żn)╗»│╔ŠĆČ╬┼cŠĆČ╬Ą─ĻP(gu©Īn)ŽĄŻ¼║▄╚▌ęū┐┤│÷Ī„ADE║═Ī„BCE×ķĄ╚ĮŪ╚²ĮŪą╬����Ż¼╝┤AD=AE=5ĪóBE=BC=5�ĪŻÅ─Č°└^└m(x©┤)Ū¾Ą├AB=10Ż¼į┘└¹ė├╣┤╣╔Č©└Ē╗“š▀Ą╚├µĘeĘ©Ū¾Ą├Ī„ADEĄ─AE▀ģ╔ŽĄ─Ė▀(ę▓×ķŲĮąą╦─▀ģą╬Ą─Ė▀)�����Ż¼Å─Č°Ū¾Ą├ŲĮąą╦─▀ģą╬Ą─├µĘe�����Ż¼įö╝Üšł┐┤▒ŠŅ}ĮŌĘ©ę╗�����ĪŻ
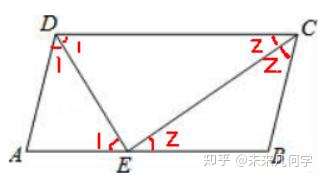
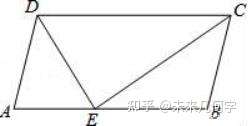
└²1 łD1-2
└²1 łD1-3
ĘĮĘ©ę╗Ż║▀^³cDū„DF⊥ABė┌³cF���Ż¼
Ī▀DE��ĪóCEĘųäe╩Ū∠ADC����Īó∠BCDĄ─ŲĮĘųŠĆŻ¼ (╩ūŽ╚Å─ĻP(gu©Īn)µIšZŠõĮŪŲĮĘųŠĆ╚ļ╩ų)
∴∠ADE=∠CDE�Ż¼∠DCE=∠BCEŻ¼
Ī▀╦─▀ģą╬ABCD╩ŪŲĮąą╦─▀ģą╬���Ż¼
∴ABĪ╬DC�Ż¼AD=BC=5��Ż¼
∠CDE=∠DEA�����Ż¼∠DCE=∠CEB����Ż¼ (į┘└¹ė├ŲĮąąŠĆĄ─ąį┘|(zh©¼)Ż¼šę│÷╦∙ėąŽÓĄ╚Ą─ĮŪ)
∴∠ADE=∠AED���Ż¼∠CBE=∠BEC��Ż¼ (Ą╚┴┐┤·ōQ����Ż¼šę│÷Ą╚č³╚²ĮŪą╬)
∴DA=AE=5Ż¼BC=BE=5����Ż¼ (░čĮŪĄ─ĻP(gu©Īn)ŽĄ▐D(zhu©Żn)╗»│╔ĮŪĄ─ĻP(gu©Īn)ŽĄ)
∴AB=10Ż¼
ätDF=DE®üEF=AD®üAF�����Ż¼
╣╩6®üFE=5®ü(5®üEF)����Ż¼
ĮŌĄ├Ż║EF=3.6����Ż¼
ätDE==4.8Ż¼
╣╩ŲĮąą╦─▀ģą╬ABCDĄ─├µĘe╩ŪŻ║4.8×10=48.
╣╩▀xŻ║C.
ĘĮĘ©Č■Ż║«öś╦│÷╦∙ėąŽÓĄ╚Ą─ĮŪęį║¾Ė∙ō■(j©┤)ŲĮąą╦─▀ģą╬Ą─ąį┘|(zh©¼)����Ż¼╬ęéā░l(f©Ī)¼F(xi©żn)∠1+∠2=90Ż¼─Ū├┤∠DEC=90;ę“×ķDC=AE+EB=10,DE=6Ż¼ĮŌĄ├Ż║CE=8;╦∙ęįŲĮąą╦─▀ģą╬├µĘe×ķ2▒Čų▒ĮŪ╚²ĮŪą╬DECĄ─├µĘe���Ż¼╝┤48�ĪŻ
▒ŠŅ}ė├ĄĮ┴╦ĮŪŲĮĘųŠĆ�ĪóŲĮąą╦─▀ģą╬ĪóŲĮąąŠĆ�����ĪóĄ╚č³╚²ĮŪą╬����Īó╣┤╣╔Č©└ĒĄ╚Ą─╗∙▒Šąį┘|(zh©¼)Ī���Ż┐┤ĄĮ?j©®ng)]����Ż¼▀@Š═šf├„┴╦Ą┌ę╗▓Į����Ż¼╩ņėøČ©┴xĪóČ©└Ē║═ąį┘|(zh©¼)ėąČÓ├┤ųžę¬!Ą½’@╚╗����Ż¼▒ŠŅ}ųąūŅųžę¬Ą─ę╗éĆŚl╝■╩ŪĮŪŲĮĘųŠĆ��Ż¼╬ęéā╔§ų┴┐╔ęį▓╗╣▄ĮY(ji©”)šōę¬Ū¾╩▓├┤��Ż¼Č°ų▒Įėė╔ĮŪŲĮĘųŠĆĄ─ąį┘|(zh©¼)ę²ī¦ś╦│÷╦∙ėąŽÓĄ╚Ą─ĮŪ�ĪŻ
šŲ╬š┴╦Ą┌Č■▓Į╚ń║╬╚ź╦╝┐╝�Ż¼100ĘųĄ─įćŠĒŻ¼75Ęųęį╔Ž╩Ū▓╗│╔å¢Ņ}┴╦�Ż¼─Ū╚ń║╬▓┼─▄½@╚ĪĖ³Ė▀Ęų─ž?ę¬╔Ųė┌╚źÜw╝{┐éĮY(ji©”)ĪŻ
Ą┌╚²▓Į�����Ż¼īWĢ■╚ń║╬╚źÜw╝{┐éĮY(ji©”)
ū÷═Ļ┴╦ę╗éĆ▌^ļy╗“š▀─ŃšJ×ķ▒╚▌^ųžę¬Ą─Ņ}─┐Ģr�Ż¼ėøĄ├╚źÜw╝{┐éĮY(ji©”)����Ż¼ą╬│╔ūį╝║Ą─ĘĮĘ©¾wŽĄĪŻ╚ń┤╦��Ż¼ęį║¾į┘ė÷ĄĮŅÉ╦ŲĄ─Ņ}─┐Ģr��Ż¼─Ń┐╔ęį║▄┐ņėąĮŌŅ}╦╝┬Ę��ĪŻ─Ū├┤į§├┤╚ź┐éĮY(ji©”)Üw╝{─ž?╬ęéā│Żė├Ą─ėąŻ║└Ēšōų¬ūR³cÜw╝{Ę©Ż¼Š▀¾wĮŌŅ}ĘĮĘ©Üw╝{Ę©�ĪŻ(ūŅ║├ėąÄūéĆŠ½ų┬Ą─ÕeŅ}▒ŠĪŻ×ķ╩▓├┤╩ŪÄūéĆ?ę“×ķ┐╔─▄įŁüĒĄ─Üw╝{▒╚▌^£\’@���Ż¼ļSų°īW┴ĢĄ─▀Mąą║═╔Ņ╚ļ����Ż¼║¾├µĄ─Üw╝{Ģ■įĮüĒįĮ║åŠÜ���Īó╚½├µ��Īó╔Ņ┐╠)
3.1��Īó└Ēšōų¬ūR³cÜw╝{Ę©
╝┤╬ęéāū÷ę╗Ą└Ņ}�����Ż¼┐╔─▄ę¬ė├ĄĮ──ą®ŽÓĻP(gu©Īn)Ą─ų¬ūR▓┼─▄ĮŌ┤│÷üĒ����ĪŻ▒╚╚ńÄū║╬Ņ}ųąŪ¾ŠĆČ╬ūŅąĪųĄ���Ż¼╬ęéāīW▀^Ą─ĻP(gu©Īn)ė┌Ū¾ŠĆČ╬ūŅąĪųĄĄ─Č©┴x����ĪóČ©└Ē╗“ąį┘|(zh©¼)┐╔ęįÜw╝{į┌ę╗ŲėąŻ║
1) ā╔³cų«ķgŠĆČ╬ūŅČ╠;
2) ³cĄĮų▒ŠĆĄ─ŠÓļx┤╣ŠĆČ╬ūŅČ╠;
3) ╚²ĮŪą╬ā╔▀ģų«▓ŅąĪė┌Ą┌╚²▀ģŻ¼ā╔▀ģų«║═┤¾ė┌Ą┌╚²▀ģ�����ĪŻ
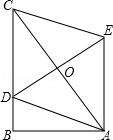
╬ęéāį┘üĒ┼eéĆ└²ūė�����Ż¼┐┤ę╗┐┤��ĪŻ
└²2�����Īó╚ńłD�����Ż¼į┌RtĪ„ABCųą�Ż¼∠B=90°���Ż¼AB=3�����Ż¼BC=4�����Ż¼³cDį┌BC╔Ž��Ż¼ęįAC×ķī”ĮŪŠĆĄ─╦∙ėąADCEųą����Ż¼DEūŅąĪĄ─ųĄ╩Ū(ĪĪĪĪ)
A.2 B.3 C.4 D.5
└²2 łD2-1
ĪŠ╦╝┐╝Ī┐ĮY(ji©”)šōę¬Ū¾ŠĆČ╬ūŅąĪųĄŻ¼─Ū╬ęéā─X║ŻųąŠ═ę¬ĖĪ¼F(xi©żn)│÷�����Ż¼Ū¾ŠĆČ╬ūŅąĪųĄėąęį╔Ž╚²ĘNČ©└Ē┐╔ęįæ¬(y©®ng)ė├��ĪŻ─Ū├┤▒ŠŅ}ę¬ė├──éĆČ©└Ē─ž?╬ęéā└^└m(x©┤)Ęų╬÷Ż║
╬ęéāšę│÷Ņ}─┐ųąĄ─ĻP(gu©Īn)µIšZŠõŻ║ęįAC×ķī”ĮŪŠĆĄ─╦∙ėąADCEųą�ĪŻ╬ęéāų¬Ą└ŲĮąą╦─▀ģą╬Ą─ī”ĮŪŠĆ╗źŽÓŲĮĘųŻ¼Ū¾DEūŅČ╠�����Ż¼ę▓Š═╩ŪŪ¾DOūŅČ╠����Ż¼─Ū├┤«öDO╩▓├┤Ģr║“ūŅČ╠─ž?O³c║═BCČ╝╩Ū╣╠Č©Ą─����Ż¼─Ū├┤ų╗ėą«öOD⊥BCĢr���Ż¼ė╔┤╣ŠĆČ╬ūŅČ╠┐╔ų¬���Ż¼┤╦ĢrŻ¼DOūŅČ╠�Ż¼ę▓╝┤DEŠĆČ╬╚ĪūŅąĪųĄ.

║▄ČÓ═¼īW┐┤ĄĮäe╚╦Ą─ĮŌ╬÷Ż¼ėXĄ├ūį╝║Č«┴╦���Ż¼Š═╚ėĄ¶▓╗╣▄┴╦���ĪŻ▓╗ę¬ęį×ķ┐┤ĄĮĮŌ╬÷Ż¼─ŃŠ═šµČ«┴╦����ĪŻ╚ń╣¹▀@Ą└Ņ}─┐─Ńķ_╩╝ø]ū÷│÷üĒŻ¼╗“š▀ĮŌŅ}ĢrŪ¦Ņ^╚fŠw��Ż¼╗©┴╦║▄ķLĢrķg▓┼ū÷│÷üĒ�Ż¼─Ū├┤▀@éĆĢr║“─ŃŠ═ę¬╚źÜw╝{┴╦Ż¼░č╦³ā╚(n©©i)╗»│╔ūį╝║Ą─¢|╬„��ĪŻ
į§├┤Üw╝{─ž?
╩ūŽ╚į┌ÕeŅ}▒Š╔Ž┴ą│÷Äū║╬Ņ}ųąŪ¾ŠĆČ╬Ą─ūŅąĪųĄ��Ż¼ŽÓĻP(gu©Īn)Ą─Č©┴x���ĪóČ©└Ē║═ąį┘|(zh©¼)(╔Ž├µęč┴ą│÷�Ż¼┤╦╠Ä▓╗į┘ųžÅ═(f©┤))╚╗║¾į┘░č├┐ĘNŪķørŽ┬├µČ╝ī”æ¬(y©®ng)īæéĆÄūĄ└└²Ņ}�����Ż¼ĘĮ▒Ń╬ęéāÅ═(f©┤)┴ĢĢrī”ššų°╚ź╦╝┐╝���ĪŻ
3.2�����ĪóŠ▀¾wĘĮĘ©Üw╝{Ę©
╝┤╬ęéāū÷─│ę╗ŅÉŅ}�Ż¼ąĶę¬ė├ĄĮ╩▓├┤ĘĮĘ©?▒╚╚ń╬ęéā┼÷ĄĮųą³c�ĪóĮŪŲĮĘųŠĆĄ╚Ą╚į§├┤╚źū÷▌oų·ŠĆ?┐┤ĄĮ30Īó45�Īó60╠ž╩ŌĮŪŻ¼╗“š▀╠ž╩ŌųĄĢr�Ż¼╬ęéā╩ūŽ╚æ¬(y©®ng)įō┬ō(li©ón)ŽļĄĮ╩▓├┤?╗“š▀╩ūŽ╚ę¬ū÷╩▓├┤?
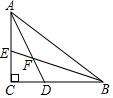
╬ęéāį┘üĒ┐┤ę╗Ą└Ņ}Ż║
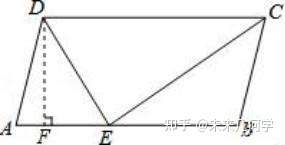
└²3��Īóį┌RtĪ„ABCųą����Ż¼∠C=90°�Ż¼ADŲĮĘų∠CABŻ¼BEŲĮĘų∠ABC��Ż¼AD��ĪóBEŽÓĮ╗ė┌³cF���Ż¼ŪęAF=4���Ż¼EF=Ż¼ätAC=——
łD └²3-1
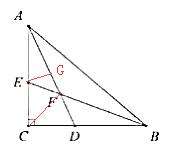
ĪŠ╦╝┐╝Ī┐┐┤ĄĮŅ}─┐ųąėąŠĆČ╬ķL×ķ�����Ż¼╬ęéāŠ═┐╔ęįęį┤╦üĒ┼ąöÓ╩Ūʱėąęį┤╦ŠĆČ╬×ķę╗▀ģĄ─╠ž╩ŌĮŪ×ķ45─ž?╚ń╣¹ėą�Ż¼╬ęéāŠ═┐╔ęįęį┤╦▀ģ×ķų▒ĮŪ╚²ĮŪą╬Ą─ą▒▀ģśŗ(g©░u)įņų▒ĮŪ╚²ĮŪą╬ĪŻ╬ęéā╩ūŽ╚üĒ┐┤Ņ}─┐ųąĄ─ĻP(gu©Īn)µIšZŠõŻ║ADŲĮĘų∠CAB��Ż¼BEŲĮĘų∠ABCŻ¼AD�����ĪóBEŽÓĮ╗ė┌³cF��ĪŻėąā╔ŚlĮŪŲĮĘųŠĆĮ╗ė┌ę╗³cĢr�Ż¼│Ż▀BĮėĄ┌╚²éĆĒö³c┼cĮŪŲĮĘųŠĆĄ─Į╗³c;▓óė^▓ņ╚²ĮŪą╬ā╔ĮŪ║═Ą─ę╗░ļ╩Ūʱ×ķ╠ž╩ŌĮŪ���Ż¼║▄’@╚╗�����Ż¼∠FAB+∠FBA=45°�����Ż¼╦∙ęįė╔═ŌĮŪČ©└Ē┐╔Ą├∠AFE=45° ���ĪŻ╚╗║¾į┘ęįEF×ķą▒▀ģśŗ(g©░u)įņų▒ĮŪ╚²ĮŪą╬Ż¼╝┤▀^Eū„EGADė┌³cG���ĪŻ
łD └²3-2
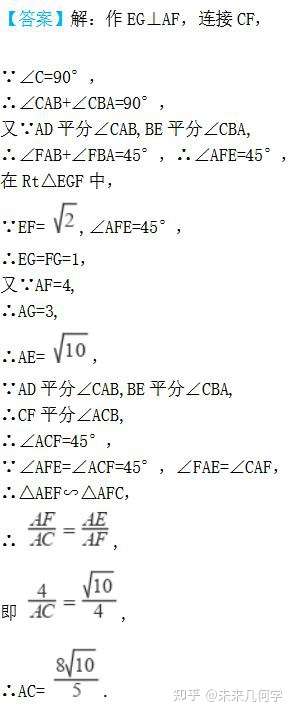
─Ū├┤═©▀^▀@éĆŅ}─┐╬ęéāŠ═┐╔ęįÜw╝{┐éĮY(ji©”)│÷ę╗éĆĘĮĘ©Ż║
┐┤ĄĮŅ}─┐ųąėąŠĆČ╬ķL×ķ�ĪóĄ╚╠ž╩ŌųĄĢrŻ¼╬ęéāŠ═┐╔ęįęį┤╦üĒ┼ąöÓ╩Ūʱėąęį┤╦ŠĆČ╬×ķę╗▀ģĄ─45�����Īó60Ą─╠ž╩ŌĮŪ��ĪŻ╚ń╣¹ėą���Ż¼╬ęéāŠ═┐╔ęįęį┤╦▀ģ×ķų▒ĮŪ╚²ĮŪą╬Ą─ą▒▀ģ╗“ų▒ĮŪ▀ģüĒśŗ(g©░u)įņų▒ĮŪ╚²ĮŪą╬�����ĪŻ
......
┐┤ĄĮ?j©®ng)]���Ż¼┐éĮY(ji©”)ČÓ┴╦Ż¼ą╬│╔ūį╝║Ą─ų¬ūR¾wŽĄ�Ż¼Ģr│Ż£ž╣╩Č°ų¬ą┬Ż¼Ž┬┤╬į┘┼÷ĄĮ▀@ŅÉŅ}─┐�����Ż¼Š═Ģ■ą╬│╔Śl╝■░l(f©Ī)╔õ����Ż¼Ž┬╣P╚ńėą╔±!
ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC����ĪóŲĮ░ÕĄ╚ęŲäėįO(sh©©)éõįLå¢ųą┐╝ŠW(w©Żng)���Ż¼2023ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą��ŻĪ>>³cō¶▓ķ┐┤